We will investigate the idea of approximating the volume of a solid generated by a function f(x,y) and axes in 3Dspace.  As our example we will use  

The idea is to sum up square prisms in this solid to approximate the volume. 

Each prism that we use will have a base 1/2 by 1/2 for a base area of 1/4.  The height of each prism will be evaluated at the center of each square. 

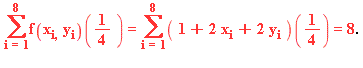
Double Integrals 

Now we will look at summing up using double integrals to evaluate the volume. 

V =  

=  

=  

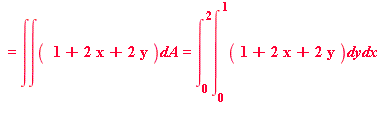
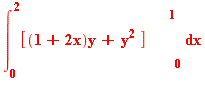
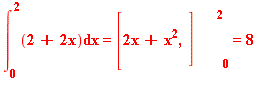
Note:  Had we used as our example a nonplanar function such as a quadratic, there would have been a difference between our summing up of the square prisms and the actual volume evaluated using double integrals is due to using the middle of the prisms as the height, as well as using only 8 such prisms. 

Below is a 3D rendering of our solid.  The Maple code I used is evidenced.  I used the structure POLYGON to create it. 

PLOT3D(POLYGONS([[0,0,0],[2,0,0],[2,1,0],[0,1,0]], 

                [[0,0,0],[0,0,1],[2,0,5],[2,0,0]], 

                [[0,0,0],[0,1,0],[0,1,3],[0,0,1]], 

                [[0,1,0],[2,1,0],[2,1,7],[0,1,3]], 

                [[2,0,0],[2,1,0],[2,1,7],[2,0,5]],
                [[0,0,1],[2,0,5],[2,1,7],[0,1,3]]),
                STYLE(PATCH),COLOR(ZHUE),AXES(BOXED)); 

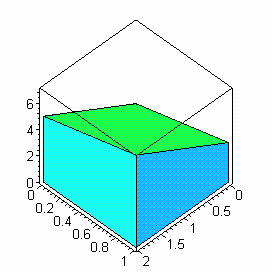
Below is a screen capture using SnagIt 8 software.  The screen is from Scientific Notebook.